That was a good one
For the love of dog, you can’t solve this problem without making assumptions that fundamentally change the answer. People are too quick to spot the first error and then make assumptions that are conveniently consistent with the correction.
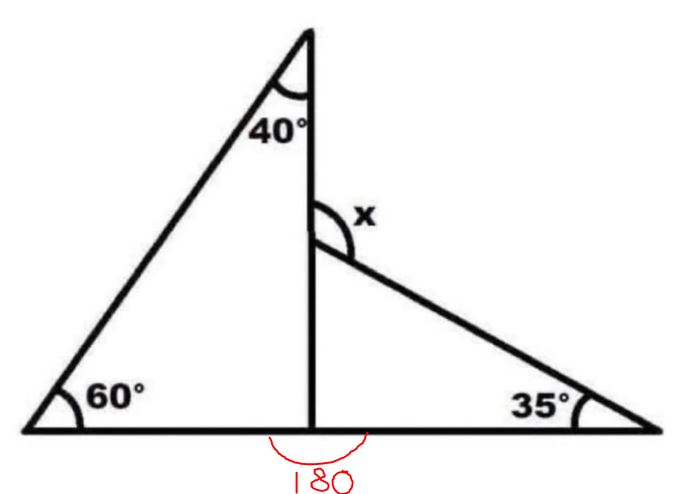
The only assumption needed to solve the problem is that the bottom line is indeed straight. Generally it will never be assumed in these types of learning practices that a straight line is a lie, because at that point you can never do a single problem ever. However an undefined angle can be cheesed.
Though it still bugs me on a fundamental level they will cheese the angle to bait a person into a wrong answer, it can teach a valuable lesson about verifying information.
We can solve this issue of a straight line being guaranteed by doing this. This actually is probably a really good practice considering the exacting nature of certain disabilities such as ADHD and Autism. However if you live in the US you need to just accept things like this because we will NEVER fund public education properly let alone consider accessibility beyond things mandated by the ADA
Heheheh the 2 triangles are having segs
40 + 60 + 35 Godamn It’s kids math.
The angle formerly known as twitter
Either this is drawn wrong or they broke geometry
The triangles aren’t drawn to scale. The middle line isn’t a 90° angle, because it isn’t specifically marked with a square angle in the corner. Triangles always add up to 180°, so the angle in the left triangle is actually 80°, not 90°.
the answers here assume that the base is a continuous, straight line
given one of the angles on the left triangle is a right angle on the diagram, but 80 if you calculate it, you can’t assume that
This is a standard way to draw geometric proofs, it’s not at all unreasonable to assume straight lines and unrepresentative angles.
normally in a geometric proof, a right angle is a right angle
This was certainly not my experience in high school. An unlabelled angle could never be assumed. Only angles marked with a square could be taken as right angles.
guess you’re right!
135
Right one does not depend on the left one. 3rd dimension for the win!
There’s perils in being in 3d
And thinking so much differently.
All these people saying its 135 are making big assumptions that I think is incorrect. There’s one triangle (the left one) that has the angles 40, 60, 80. The 80 degrees is calculated based on the other angles. What’s very important is the fact that these triangles appear to have a shared 90 degree corner, but that is not the case based on what we just calculated. This means the image is not to scale and we must not make any visual assumptions. So that means we can’t figure out the angles of the right triangle since we only have information of 1 angle (the other can’t be figured out since we can’t assume its actually aligned at the bottom since the graph is now obviously not to scale).
Someone correct me if I’m wrong.
Stupid stuff like this is why kids hate math class. Unless the problem says calculate all unmarked angles, those visually 90 degree angles are 90 degrees. It works that way in any non engineering job that uses angles because it’s common sense.
…what? I get that this drawing is very dysfunctional, but are you going to argue that a triangle within a plane can have a sum of angles of 190°?
Nope I’m not saying that. I’m saying this is a gotcha question that demotivates learners.
I see. I agree completely. The only place this belongs is as a thought experiment on making assumptions in geometry.
No, they’re saying that unless you’re already good at this stuff, it’s easy to assume that a visually 90° angle is actually 90° even when it’s not
The sum of the angles of a triangle are always 180°
Yes, I believe I implied this by suggesting that the sum of angles being 190° is absurd.
You’re making the assumption that they are triangles.
This is a standard way to draw geometric proofs, it’s not at all unreasonable to assume straight lines alongside unrepresentative angles. It’s certainly still an assumption, but a conventional one.
Your assumption is that it’s a Cartesian coordinate system with 90° angles. But that’s not necessarily the case. You can apply a sheer transformation to correct for the unusual appearance. When you do that, the angles change, but straight lines stay straight and parallels stay parallel. There’s a mathematical term for that, which I can’t remember right now.
I mean, the assumption shouldn’t be anything about scale. It should be that we’re looking at straight lines. And if we can’t assume that, then what are we even doing.
But, assuming straight lines, given straight lines you find the other side of an intersecting line because of complements.
We can’t assume that the straight line across the bottom is a straight line because the angles in the drawing are not to scale. Who’s to say that the “right angle” of the right side triangle isn’t 144°?
If the scale is not consistent with euclidian planar geometry, one could argue that the scale is consistent within itself, thus the right triangle’s “right angle” might also be 80°, which is not a supplement to the known 80° angle.
And if we can’t assume that, then what are we even doing
That’s exactly what the other user is saying. We can’t assume straight lines because the given angles don’t make any sense and thus this graph is literally impossible to make. We’re arguing over literal click bait is what we’re doing.
Why do the labeled angles prevent us from assuming straight lines?
Because the apparently straight lines contradict the labels. As drawn, the unlabeled bottom vertices are clearly 90°, not 80° and 100°. We must either conclude that the labels are incorrect, or that the figure is not drawn to scale. Either way, it’s insoluble.
Because the angles aren’t represented accurately. It could be that the two angles that look like they’re 90° add up to 180°, but they could also not
That’s technically possible, but that’s also an irrational take. The rational take is to assume the problem is solvable given the available information, which means assuming that the lines are straight.
Yes, two angles appear to be 90⁰, but they’re obviously not with the given information. Math conventions nearly always label right angles, so not having the right angle there implies that the angle should not be assumed to be 90⁰. Math conventions in trigonometry also generally assume straight lines unless there’s a visual indicator that they’re not, and those tend to be exaggerated so it’s obvious.
So the rational answer here is that the bottom line is straight and therefore the problem is solvable. Saying otherwise is irrational, because that’s so far away from math conventions.
I’d argue that the bottom line is indeed one continuous line regardless of how many other lines intersect on it, because there’s nothing indicating that the line is broken at the intersection.
Now the only reason I think the lines are straight at all is use of the angular notations at the ends, which would be horribly misleading to put at the end of curves or broken lines.
135 is correct. Bottom intersection is 80/100, 180-35-100 = 45 for the top of the second triangle. 180 - 45 = 135
Mathematician here; I second this as a valid answer. (It’s what I got as well.)
Random guy who didn’t sleep in middle school here: I also got the same answer.
Random woman who didn’t sleep very well last night. I got a different answer, then thought about it for 10 more seconds and then got 135.
(No I didn’t assume the right angle, my mistake was even dumber. I need a nap.)
You’re making the assumption that the straight line consisting of the bottom edge of both triangles is made of supplementary angles. This is not defined due to the nature of the image not being to scale.
Unless there are lines that are not straight in the image (which would make the calculation of x literally impossible), the third angle of the triangle in the left has to be 80°, making the angle to its right to be 100°, making the angle above it to be 45°, making the angle above it to be 135°. This is basic trigonometry.
I ask you to consider the following picture:
I tell you that the triangles are not to scale. We can definitively say that h = 80° and k = 90°. Note that h + k != 180°. Despite the strange and inconsistent scaling, this meets all requirements of triangles.Now let me take away the defined 50° angle:
Once again, the triangles are not to scale. They are visually the same triangles. You might assume that h + k = 180°, yielding 40° for the missing angle above k. However, if I reveal to you that the missing angle is indeed 50° or 60° or ANY ANGLE (excl. 40°) such that the sum of angles can still be 180°, you and your assumption are suddenly wrong.Perhaps consider nurturing your brain further before making such condescending remarks.
Following your logic, there is no evidence that these are triangles and it is never stated, therefore none of these lines might be straight and the discussion is irrelevant.
You’re overlooking a major assumption on your end. There is nothing in the image that suggests that the bottom of both triangles forms a straight line. The pair of bottom edges are two separate lines. They may or may not form a sum 180° angle. You are assuming the angles are supplementary. We know that the scale of the image is wrong, thus it is not safe to definitively say that the 80° angle’s neighbor is supplementary. They may be supplementary, or the triangles may share a consistently skewed scale, or the triangles may each have separately skewed scales.
This is a basic logical thought process.
What you say makes no sense.
The problem is LITERALLY unsolvable if we can’t assume that all the lines are straight.
The schematic was OF COURSE purposefully drawn in a way to make the viewer assume that the third angle of the left triangle is 90°, making the angle to it’s right also be 90°, but the point of the exercise is to get the student to use ALL the given information instead of presuming right angles.
And NO, assuming all the lines are straight is NOT unreasonable, it is the only way that the problem could ever possibly have a solution.
And NO, assuming all the lines are straight is NOT unreasonable, it is the only way that the problem could ever possibly have a solution.
Wow, you got so close to my point but still fell short! My point is that you cannot reach a solution without making assumptions that fundamentally alter the solution. Your math is correct if and only if your straight line assumption is true. It may be a reasonable assumption, but that does not mean it must always be an accurate assumption.
Reasonable assumptions are a fundamental requirement for communication. It’s not that you are wrong in what you are saying. There is a chance that the poser of the question made a visual representation of the triangle’s sides appear to be complementary and appear to construct a straight line across their bases while not actually definitively indicating them as such.
The way these triangle’s are represented is already skewed so perhaps that is what they are trying to do.
The thing is though, at that point they are defying convention and reasonable assumptions so much that they aren’t worth engaging seriously because it’s flawed communication.
The version people are choosing to answer seriously is equivalent to a guy holding up a sign that says “ask me about my wiener to get one in a flash for free!” while standing next to a hot dog stand. If you ask he flashes his junk at you and says cheekily “haha you just assumed wrong! Idiot!”
That’s already dumb enough but some people could see the clues that suggest he was actually intended to flash people the whole time through a series of reasonable assumptions about his outfit lacking pants or the hit dog stand not even being turned on.
Your argument that we can’t assume the line at the bottom is straight is like saying we can’t assume the theoretical trenchcoat man won’t toss a rabid dachshund he was hiding under the coat at us because the hot dog stand has no buns or condiments on it.
You might not be provably wrong but it’s really not worth thinking like an insane person just because a few conventions were defied
I’d say that the shape on the left has what appears to be a little kink right near X, so one might infer that the shape on the left might be a quadrilateral. There are blatantly obvious vertices that are not labeled as such, so we can’t assume that the not-quite-straight line is supposed to be straight since other angles are also not explicitly indicated as vertices…
There is nothing in the image that suggests that the bottom of both triangles forms a straight line.
Except for the part where it’s a single straight line segment, as depicted in the image. Showing the complimentary angles as an unlabeled approximately right angle is within convention. Showing a pair of line segments that do not form a straight line as a straight line is not.
Exactly.
Add to this that
xis literally impossible to calculate if conventions are not assumed, and absolutely possible to calculate if conventions are followed. Assuming the conventions won’t hold is an irrational position.
which would make the calculation of x literally impossible
Yes.
But that doesn’t mean that line must be straight. It just means if it isn’t, you can’t derive x.
I got 55
What a deviously misleading diagram.
The triangle on the left isn’t actually a right angle triangle, as the other angles add to 100°, meaning the final one is actually 80°, not 90°.
Therefore the triangle on the right also isn’t a right angle triangle. That corner is 100°.
100+35=135°. 180-135=45°. So that’s 45° for the top angle.
X = the straight line of the joined triangles (180°) - the top angle of the right triangle (45°). 180-45=135°
X is 135°, not the 125° it initially appears to be.
I looked at that “90°” angle and went “that doesn’t look right…”
Leave it to the Grand Nagus to spot a clever ruse.
12th rule of acquisition : let assumptions work in your favor
The person who made it needs this:
It’s a geometry puzzle. Of course they aren’t going to get out a protractor to carefully get the 80° drawn to scale. The point of these puzzles isn’t that we actually want to know what the angle is. The point is to navigate a maze of logic. (A very short maze in this particular case.)
Yes, and in this case, the puzzle was poorly presented and likely unsolvable.
I… don’t understand it ?
With proper punctuations: There are three words in “the English language”. The other half of it is supposed to be a misdirection.
But yeah, the original joke was really bad in the first place. I don’t blame the second guy for his reaction.
It literally explains it in the comic? People who communicate badly and then act smug when they’re misunderstood are annoying. The other user is saying that the same applies to the OPs post; because the angles don’t match the graphic, they’re communicating badly
Yes but what is communicated badly ? What did the riddle man mean by the three words in english language that end in “gry” ?
The “Riddle Man” wants the answer to be ‘language’ because the question he claims to have asked is what’s the third word in “the English Language.”
If we credulously try to answer the implied question, it’s better to just link this page, but you read the whole thing.
https://www.merriam-webster.com/help/faq-third-common-gry-word
As the explain xkcd notes, it’s badly told by cueball so it’s impossible to answer. https://www.explainxkcd.com/wiki/index.php/169:_Words_that_End_in_GRY
https://www.explainxkcd.com/wiki/index.php/169:_Words_that_End_in_GRY
I don’t know if that helps or not.
It also doesn’t say that the line on the bottom is straight, so we have no idea if that middle vertex adds up to 180 degrees. I would say it is unsolvable.
This is what I was thinking. The image is not to scale, so it is risky to say that the angles at the bottom center add up to 180, despite looking that way. If a presented angle does not represent the real angle, then presented straight lines might not represent real lines.
Eh, I think @sag pretty well nailed it.
Looks like an outer triangle with inner triangles so x = 180 - (180 - (40 + 60 + 35)) = 40 + 60 + 35 = 135
Can you clarify what you mean? this doesn’t make sense to me. There isn’t an “outer” triangle. There’s one triangle (the left one) that has the angles 40, 60, 80. Both triangles are misleadingly drawn as they appear to be aligned at the bottom but they’re not (left triangle’s non-displayed angle is 80, not 90 degrees). So that means we can’t figure out the angles of the right triangle since we only have information of 1 angle (the other can’t be figured out since we can’t assume its actually aligned at the bottom since the graph is now obviously not to scale).
I used to have teacher who deliberately made disproportionate diagrams. His reasoning was that people trust too much what their eyes see and not enough what the numbers tell them. He would’ve loved that diagram.
I thought is was wierd that my math didn’t make sense, thanks!
I like that all the comments are people discussing the diagram.
Seeing the other comments, it might be worth a shot to repost this meme with your math homework thrown in for easy solutions.
Of course, I did the math too before looking.
Unfortunately, nobody can define a true answer without making assumptions, which is a thought process shown to be faulty by the false right angles.
